Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en ecuaciones diferenciales ordinarias y ecuaciones en derivadas parciales.
-Tipos:
- Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
- Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
Una ecuación diferencial es una ecuación que incluye expresiones o términos que involucran a una función matemática incógnita y sus derivadas. Algunos ejemplos de ecuaciones diferenciales son:
- es una ecuación diferencial ordinaria, donde
 representa una función no especificada de la variable independiente
representa una función no especificada de la variable independiente  , es decir,
, es decir,  ,
,  es la derivada de
es la derivada de  con respecto a
con respecto a  .
.
- La expresión
 es una ecuación en derivadas parciales.
es una ecuación en derivadas parciales.
A la variable dependiente también se le llama función incógnita (desconocida). La resolución de ecuaciones diferenciales es un tipo de problema matemático que consiste en buscar una función que cumpla una determinada ecuación diferencial. Se puede llevar a cabo mediante un método específico para la ecuación diferencial en cuestión o mediante una transformada (como, por ejemplo, la transformada de Laplace).
-Usos:
Las ecuaciones diferenciales son muy utilizadas en todas las ramas de la ingeniería para el modelado de fenómenos físicos. Su uso es común tanto en ciencias aplicadas, como en ciencias fundamentales (física, química, biología) o matemáticas, como en economía.
- En dinámica estructural, la ecuación diferencial que define el movimiento de una estructura es:
Donde M es la matriz que describe la masa de la estructura, C es la matriz que describe el amortiguamiento de la estructura,K es la matriz de rigidez que describe la rigidez de la estructura, x es vector de desplazamientos [nodales] de la estructura,P es el vector de fuerzas (nodales equivalentes), y t indica tiempo. Esta es una ecuación de segundo orden debido a que se tiene el desplazamiento x y su primera y segunda derivada con respecto al tiempo.
- La vibración de una cuerda está descrita por la siguiente ecuación diferencial en derivadas parciales de segundo orden:
donde 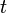 es el tiempo y
es el tiempo y  es la coordenada del punto sobre la cuerda. A esta ecuación se le llama ecuación de onda.
es la coordenada del punto sobre la cuerda. A esta ecuación se le llama ecuación de onda.
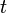 es el tiempo y
es el tiempo y  es la coordenada del punto sobre la cuerda. A esta ecuación se le llama ecuación de onda.
es la coordenada del punto sobre la cuerda. A esta ecuación se le llama ecuación de onda.


Muy bien Unai, se ve que has trabajado.
ResponderEliminar